En el anterior post titulado Ejemplo de uso de DBSCAN en Python para eliminación de outliers se vio cómo ejecutar un algoritmo DBSCAN para detección de outliers en Python; sus parámetros se eligieron de forma más o menos visual a partir de la nube de puntos y de la curva elbow.
El problema que esto representa es que, para cada caso, hay que determinar de forma visual que par de parámetros (min_pts y eps) son los adecuados. En esta entrada propongo un sencillo método creado por mi, que calcula de forma automática los parámetros min_pts y eps de DBSCAN.
Este método creo que puede ser aplicable para la limpieza de cualquier curva que siga una tendencia y por tanto incluya una zona muy densa de puntos (la curva o recta principal) y otra u otras zonas menos densas que representan outliers alrededor de la tendencia principal. Dejo a discreción del lector probar éste método en nubes de puntos con diferentes configuraciones.
Para el ejemplo propuesto, eliminaremos los outliers de las señales Irradiancia/Rendimiento de una instalación fotovoltaica y se programará todo en R.
1. Acerca de la parametrización de DBSCAN
DBSCAN se parametriza con dos valores: un número épsilon (eps) positivo y un número natural minPoints (min_pts). El algoritmo parte de un punto arbitrario en el conjunto de datos; si hay una cantidad de puntos mayor o igual a min_pts a una distancia eps del punto arbitrario, a partir de ese momento se consideran todos los puntos como parte de un clúster.
A continuación, se expande ese grupo mediante la comprobación de todos los nuevos puntos y ver si ellos también tienen más puntos min_pts a una distancia eps, creciendo el clúster de forma recursiva en caso afirmativo.
A medida que se generan los clústeres, quedan puntos sin añadir. A continuación, se elige un nuevo punto arbitrario y se repite el proceso. Es posible que el punto arbitrario escogido tenga menos de min_pts puntos en su círculo de radio eps, y tampoco sea parte de cualquier otra agrupación. Si ese es el caso, se considera un «punto de ruido» o outlier que no pertenece a ningún grupo.
2. Datos iniciales.
Cargamos las librerías a usar y los datos para el ejemplo:
library(dbscan)
library(dplyr)
library(scales)
# Carga de datos
datos <- readRDS("datos.rds")
La librería dbscan la utilizaremos, evidentemente, para usar el algoritmo DBSCAN. La librería dplyr la utilizaremos para realizar algunas operaciones sencillas con el dataframe y por último, la librería scales la utilizaremos para normalizar los datos.
Partimos de un dataset de 2300 observaciones y 2 variables guardado con el nombre «datos», que son la Irradiancia solar y el rendimiento obtenido. Presuponemos que tenemos unos datos «limpios», sin valores NA o valores inválidos como + ∞ ó – ∞.

La curva Irradiancia/Rendimiento queda de la siguiente forma:
plot(datos$Irradiancia, datos$Rendimiento, ylab = "Rendimiento", xlab = "Irradiancia solar", col = "red")

Como se puede observar, hay datos alejados de la curva que son claramente outliers, incluso algunos con rendimiento superior al 100%. Aplicaremos DBSCAN para detectar y eliminar dichos valores anómalos.
3. Cálculo de min_pts.
El parámetro min_pts establece el número de puntos mínimo que, dado un radio eps, tiene que haber para que se considere que dichos puntos forman un clúster. Se podría decir, por tanto, que min_pts es una medida de “densidad” de puntos. Un valor bajo de min_pts asegurará que más puntos son agrupados, pero se corre el riesgo de agrupar outliers. Por el contrario, un valor muy alto de min_pts puede descartar valores que no son anómalos.
En general, muchos autores recomiendan usar valores de min_pts entre 3 y 5, que ciertamente funcionan bastante bien en la mayoría de los casos. La diferencia puede darse en casos «extremos» de datos pocos densos o muy densos. Para ello, mi propuesta que ha sido calculada de forma empírica para mis datos, es usar un min_pts que sea igual a un 0,20%-0,25% del total de los datos a limpiar, fijando dos valores límite:
- El min_pts mínimo será de 2 para un volumen muy pequeño de datos.
- El min_pts máximo será 10 para volúmenes altos de datos.
Poner un límite inferior impide elegir por error un min_pts de 1 (todos los puntos serían clúster) o de 0 (producirá un error). Poner un límite superior de min_pts impedirá eliminar grupos de cierta densidad pero alejados de la zona densa principal que podrían no ser outliers.
El código implementando lo anterior quedaría tal que así:
# Cálculo de min_pts
k <- 0.0020 # Porcentaje elegido.
min_pts <- round(nrow(datos) * k) # Cálculo de min_pts.
if (min_pts <= 1) { # Elimino la opción de un min_pts < 1 y limito su valor máximo.
min_pts <- 2 } else if (min_pts >= 10) {
min_pts <- 10
}
Para 2300 datos min_pts sale igual a 4,6 que se redondea a 5.
4. Normalización de datos.
Antes de proseguir, y como en cualquier algoritmo de Machine Learning basado en distancias, es necesario normalizar los datos. Usamos la función rescale() de R que normalizará nuestro dataframe entre [0, 1].
datos_norm <- data.frame(lapply(datos,rescale))
5. Cálculo de EPS
Una vez fijado min_pts, procedemos a automatizar la elección de eps. Para ello, crearemos una función llamada auto_eps() que tendrá dos argumentos de entrada: los datos y el min_pts calculado previamente. La función realiza los siguientes pasos:
- Mediante la función dbscan::kNNdist(), que sirve para realizar un cálculo rápido de las distancias k-vecinas más cercanas en una matriz de puntos, se crea una matriz de de distancias A.
- Con la función order() ordenamos esos puntos de menor distancia a mayor y lo guardamos en un vector llamado Ar. Este vector será nuestro eje Y en la curva elbow.
- Se crea otro vector, de números enteros entre [0 , length(Ar)-1] que será nuestro eje X en la curva elbow.
- Se normalizan con rescale() ambos datos entre [0, 1] para que poder calcular correctamente el siguiente paso.
- Calculo la pendiente de la recta imaginaria entre cada punto de la curva elbow con la conocida ecuación de la pendiente:
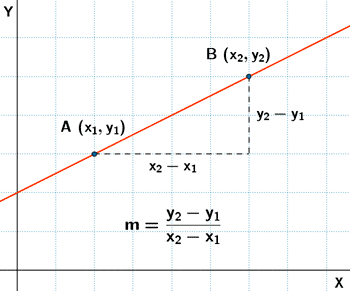
- Elijo una pendiente m en la cual el valor de eps (eje Y) varíe muchos más que el eje X, que será un valor en la zona de la curva. Dependiendo de la forma de nuestra curva, una pendiente alrededor de 10 puede darnos muy buenos resultados.

- Por último, la función auto_eps() devuelve el valor del eje Y (eps) en el que se produce el valor de la pendiente m elegido.
El código queda tal que así:
auto_eps <- function(xdf, min_pts) { # Se introduce un dataset de dos columnas normalizadas.
A <- dbscan::kNNdist(xdf, k = min_pts)
Ar <- A[order(A)]
y <- Ar
x <- c(0:(length(Ar)-1))
# Normalizo antes de calcular la curvatura.
xr <- rescale(x)
yr <- rescale(y)
curvatura <- array() # Aquí se guardarán las pendientes.
# Cálculo de pendiente.
i = 1
while (i <= length(x)) {
curvatura[i] <- (yr[i+1]-yr[i])/(xr[i+1]-xr[i])
i <- i + 1
}
# Elijo el primer valor que supere la pendiente m
m <- 10
primer <- first(which(curvatura >= m))
# Devuelve el valor eps óptimo
return(y[primer])
}
Y llamo a la función con los argumentos del dataset normalizado y el min_pts calculado anteriormente:
epsilon <- auto_eps(datos_norm, min_pts)
Para mi caso, el valor eps ha sido de 0,011943971, en el que se produce una pendiente de m = 10. Podemos ver gráficamente como se corresponde con el codo de la curva elbow:
A <- dbscan::kNNdist(datos, k = min_pts) Ar <- A[order(A)] plot(Ar) abline(h=epsilon, col = "red", lty=7)

6. DBSCAN
Con los valores min_pts y eps ya calculados, aplico DBSCAN sobre mis datos normalizados:
# DBSCAN res <- dbscan(datos_norm, eps = epsilon, minPts = min_pts)
Si escribimos res en la consola, se comprueba que se han detectado 79 outliers en un total de 2300 datos:

Ahora procedemos a etiquetar los clústers en mis datos sin originales para, posteriormente, eliminar todos aquellos que son outliers (clúster = 0):
datos$cluster = res$cluster # Añado la columna clúster a mis datos. datos_limpios <- dplyr::filter(datos, cluster != 0) # Guardo datos limpios. outliers <- dplyr::filter(datos, cluster == 0) # Guardo outliers.
Represento de nuevo la curva, esta vez marcando en rojo los puntos detectados como outliers por DBSCAN:
# Curva irradiancia/rendimiento con outliers. plot(datos_limpios$Irradiancia, datos_limpios$Rendimiento, ylab = "Rendimiento", xlab = "Irradiancia solar", col = "blue") points(outliers$Irradiancia, outliers$Rendimiento, col ="red")

Y por último represento gráficamente la curva «limpia»:
plot(datos_limpios$Irradiancia, datos_limpios$Rendimiento, ylab = "Rendimiento", xlab = "Irradiancia solar", col = "blue")
